【エクセルの住宅ローン返済予定表テンプレート無料配布中!】
エクセルで住宅ローンを計算する場合、「返済額」「元金」「利息」を求める関数を使うと、簡単に住宅ローンのシミュレーションができます。
元利均等返済と元金均等返済では、利用する関数が異なりますので、注意しましょう。
こちらでは、エクセルを使って元利均等返済と元金均等返済の「返済額」「元金」「利息」の計算方法について、わかりやすく解説しています。
- 元利均等返済と元金均等返済の比較
- 元利均等返済の「PMT」「PPMT」「IPMT」関数の使い方
- 元金均等返済の「ISPMT」関数の使い方
- 【無料配布】エクセルの住宅ローン返済予定表テンプレート
住宅ローンの返済方法
住宅ローンの返済方法には、以下の2つがあります。
- 元利均等返済
- 元金均等返済
元利均等返済と元金均等返済の比較
こちらは、元利均等返済と元金均等返済のメリット・デメリットを比較したものです。
| 元利均等返済方式 | 元金均等返済方式 | |
|---|---|---|
| 返済方法 | 元金分と利息分を合わせた金額(返済額)が毎月一定となる返済方法 | 元金分を毎月均等にして、利息と合わせて返済する方法 |
| 返済イメージ | 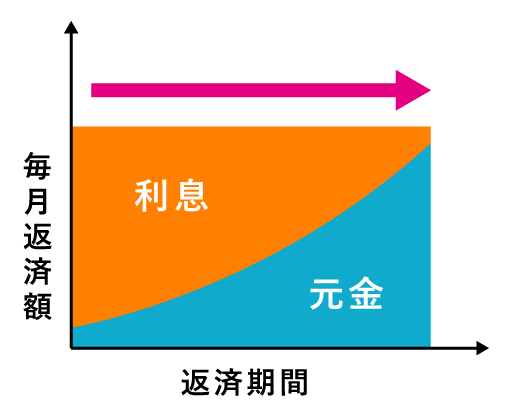 |
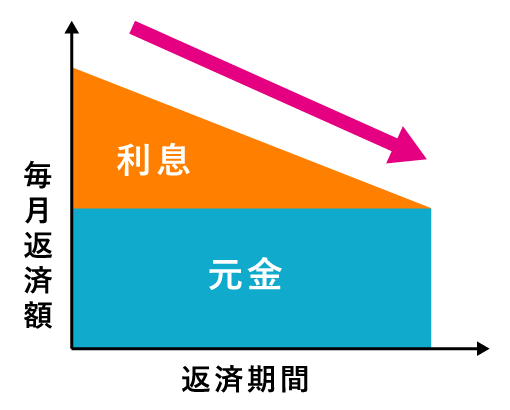 |
| メリット | ・毎月返済額が一定で、返済計画が立てやすい ・返済開始当初は、元金均等返済より返済額が少ない |
・返済が進むにつれて、毎月返済額が少なくなる ・同条件で、元利均等返済より総返済額が少ない |
| デメリット | ・同条件で、元金均等返済より総返済額が多い ・元金の減り方が遅く、利息が高い |
・返済開始当初の返済額が多い ・借入可能額が少なくなる |
返済イメージを見て分かるように、毎月の返済額に違いがあります。
つまり、元利均等返済と元金均等返済では、計算式が異なるということです。
そこで、エクセルでは、それぞれの「元金」「利息」「返済額」を求める関数が用意されています。
それぞれのエクセル関数の使い方について、詳しく解説していきます。
元利均等返済のエクセル関数

元利均等返済とは 『元金分と利息分を合わせた毎月の返済額が一定となる返済方法』のことです。
毎月の元金分と利息分を調整して、毎月の返済額が一定となるのが特徴です。
元利均等返済で使うエクセル関数
元利均等返済で使うエクセル関数は、以下の3つです。
- PMT関数・・・毎月の返済額を計算
- PPMT関数・・・毎月の元金分を計算
- IPMT関数・・・毎月の利息分を計算
毎月の返済額を求めるPMT関数
PMT関数とは 『一定利率で1回あたりの返済額を求める関数』 のことです。
元利均等返済の毎月返済額を求める場合は、PMT関数を利用します。
PMT関数の計算式は、以下の通りです。
| 項目(引数) | 詳細 |
|---|---|
| 利率(必須) | 金融機関の利率を指定 |
| 期間(必須) | 住宅ローン返済期間の返済回数合計を指定 ※「利率」と同じ単位を指定しなければいけません。 「年利1.2%→10年」「月利0.1%→120ヶ月」 |
| 現在価値(必須) | 住宅ローンの借入金額を指定 |
| 将来価値(省略可) | 住宅ローン返済では、「0」を指定 ※省略すると「0」で処理されます。 |
| 支払期日(省略可) | 支払いを「各期の期末(0)」か「各期の期首(1)」を指定 ※省略すると「0」の各期の期末で処理されます。 |
毎月の返済額を計算する場合は、「利率」「期間」「現在価値」の3つを入力すれば、求められます。
利率
利率には、毎年の返済額を求めるなら「年利」を、毎月の返済額を求めるなら「月利」を入力します。
月利とは 『借入金額に対して月単位でかかる金利』 のことです。
住宅ローンの金利は、年単位の年利で記載されていますので、月利に変換するには、12ヶ月で割ります。
例えば、金利1.2%の月利は、
となります。
期間
期間には、住宅ローン返済期間の返済回数合計を入力します。
「期間」と「利率」は、同じ単位を指定しなければいけません。
例えば、利率に年利1.2%を入力したら返済回数は10(年)、利率に月利0.1%を入力したら返済回数は120(ヶ月)となります。
現在価値
現在価値には、住宅ローンの借入金額を入力します。
借入金残高は 『返済済み元金を差し引いた借入金』のことです。
例えば、借入金3,000万円で58,000円を返済したら、借入金残高は、
になります。
ちなみに返済1回目は、まだ返済していませんので、借入金残高は「3,000万円」となります。
将来価値
将来価値は、省略可能項目で入力不要です。
将来価値には、最後の支払いが終わった後の現金を指定しますが、住宅ローン返済は支払いが完了すると将来価値は「0」です。
省略した場合は、「0」で処理されますので、入力しなくても問題ありません。
支払期日
支払期日は、省略可能項目で入力不要です。
支払期日には、「各期の期末(0)」か「各期の期首(1)」の支払期日を指定しますが、通常は期末払いのため「0」を指定します。
例えば、1月の期末払いであれば1月31日、期首払いであれば1月1日が、支払期日となります。
省略した場合は、「0」で処理されますので、入力しなくても問題ありません。
ちなみに、期首払いは、利息がかかる前に1回目の返済を行うため、期末払いよりも若干返済総額が少なくなります。
エクセルの計算式
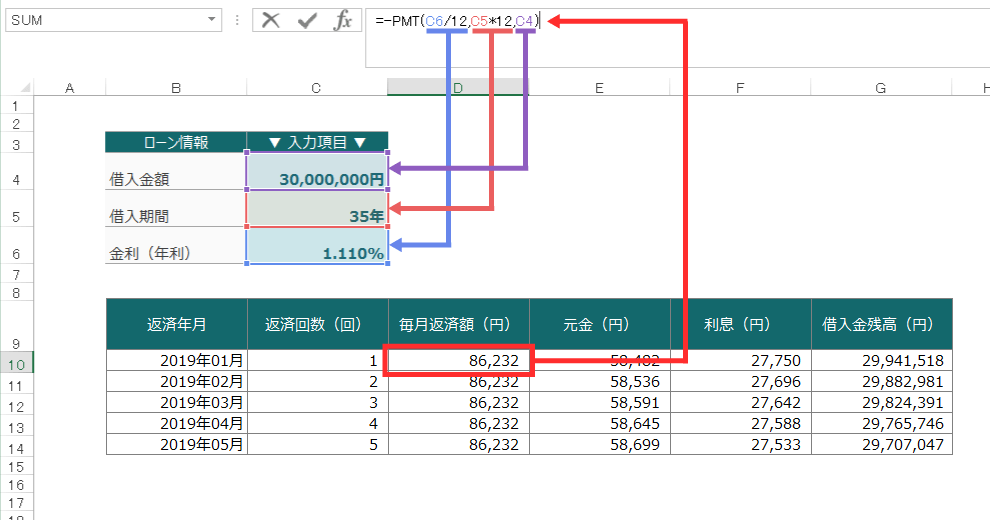
エクセルでは、このように該当するセルを参照させます。
例えば、「借入金額:3,000万円」「借入期間:35年」「金利(年利)1.110%」で計算式に代入すると
で、毎月の返済額「86,232円」が求められます。
計算式の注意点
計算式の注意点として、以下のようにPMTの前に「-(マイナス)」が入っています。
PMT関数は、返済額を手元から出て行くお金と判断して、「-」で表示されます。
マイナス表示は見づらいため、「-」に「-」をかけて、プラスに変換しています。
他にも「ABS関数」で絶対値で表示させる方法もありますが、「-」をつけたほうが早いです。
ボーナス返済
PMT関数は、1回あたりの返済額を求める関数ですので、年間返済額やボーナス返済の返済額を求めたい場合は、「年利」で計算しても問題ありません。
例えば、「借入金額(ボーナス返済分):560万円」「借入期間:35年」「金利(年利)1.110%」「年1回のボーナス返済」を考えている場合は、
で、ボーナス返済額「96,763円」が求められます。
もしも、年2回ボーナス返済を検討する場合は、
とエクセルの計算式を変更すれば、回数に応じてボーナス返済額を求めることができます。
毎月の元金分を求めるPPMT関数
PPMT関数とは 『一定利率で1回あたりの元金分を求める関数』 のことです。
元利均等返済の毎月元金分を求める場合は、PPMT関数を利用します。
PPMT関数の計算式は、以下の通りです。
| 項目(引数) | 詳細 |
|---|---|
| 利率(必須) | 金融機関の利率を指定 |
| 期(必須) | 住宅ローン返済期間のうち何回目かを指定 ※「利率」と同じ単位を指定しなければいけません。 「年利1.2%→10年」「月利0.1%→120ヶ月」 |
| 期間(必須) | 住宅ローン返済期間の返済回数合計を指定 ※「利率」と同じ単位を指定しなければいけません。 「年利1.2%→10年」「月利0.1%→120ヶ月」 |
| 現在価値(必須) | 住宅ローンの借入金額を指定 |
| 将来価値(省略可) | 住宅ローン返済では、「0」を指定 ※省略すると「0」で処理されます。 |
| 支払期日(省略可) | 支払いを「各期の期末(0)」か「各期の期首(1)」を指定 ※省略すると「0」の各期の期末で処理されます。 |
毎月の元金分を計算する場合は、「利率」「期」「期間」「現在価値」の4つを入力すれば、求められます。
利率・期間・現在価値・将来価値・支払期日
利率・期間・現在価値・将来価値・支払期日は、すべてPMT関数と内容は同じです。
期
期には、住宅ローン返済期間のうち何回目かを入力します。
例えば、返済期間35年(420回)であれば、期は「1~420」のいずれかで、5回目の元金分を計算したい場合は「5」を、23回目の元金分を計算したい場合は「23」を入力します。
エクセルの計算式
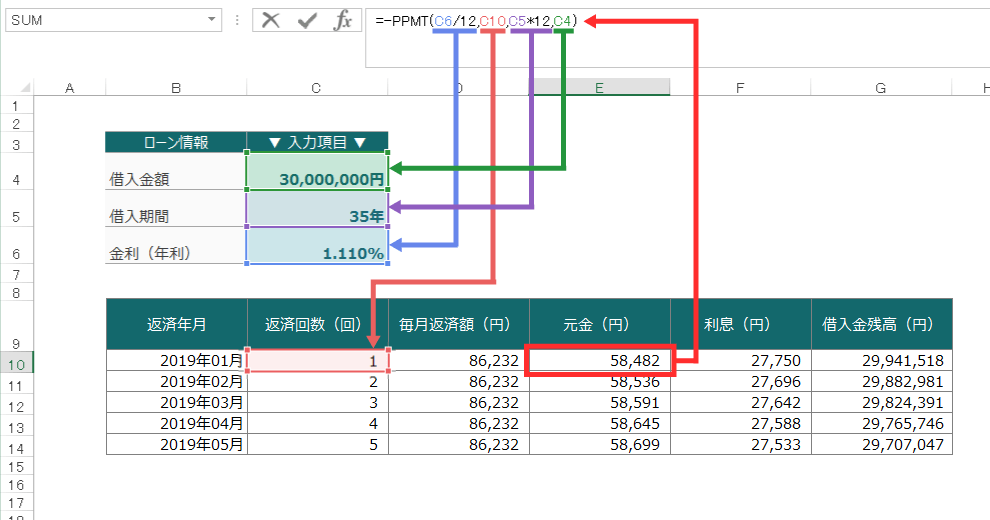
エクセルでは、このように該当するセルを参照させます。
例えば、1回目の元金分を計算する場合は、
で、「58,482円」が求められます。
15回目の元金分を計算する場合は、
と、「期」を変えていけば、知りたい期の元金分を計算できます。
毎月の利息分を求めるIPMT関数
IPMT関数とは 『一定利率で1回あたりの利息分を求める関数』 のことです。
元利均等返済の利息分を求める場合は、IPMT関数を利用します。
IPMT関数の計算式は、以下の通りです。
| 項目(引数) | 詳細 |
|---|---|
| 利率(必須) | 金融機関の利率を指定 |
| 期(必須) | 住宅ローン返済期間のうち何回目かを指定 ※「利率」と同じ単位を指定しなければいけません。 「年利1.2%→10年」「月利0.1%→120ヶ月」 |
| 期間(必須) | 住宅ローン返済期間の返済回数合計を指定 ※「利率」と同じ単位を指定しなければいけません。 「年利1.2%→10年」「月利0.1%→120ヶ月」 |
| 現在価値(必須) | 住宅ローンの借入金額を指定 |
| 将来価値(省略可) | 住宅ローン返済では、「0」を指定 ※省略すると「0」で処理されます。 |
| 支払期日(省略可) | 支払いを「各期の期末(0)」か「各期の期首(1)」を指定 ※省略すると「0」の各期の期末で処理されます。 |
毎月の利息分を計算する場合は、「利率」「期」「期間」「現在価値」の4つを入力すれば、求められます。
利率・期・期間・現在価値・将来価値・支払期日
利率・期・期間・現在価値・将来価値・支払期日は、すべてPPMT関数と内容は同じです。
エクセルの計算式
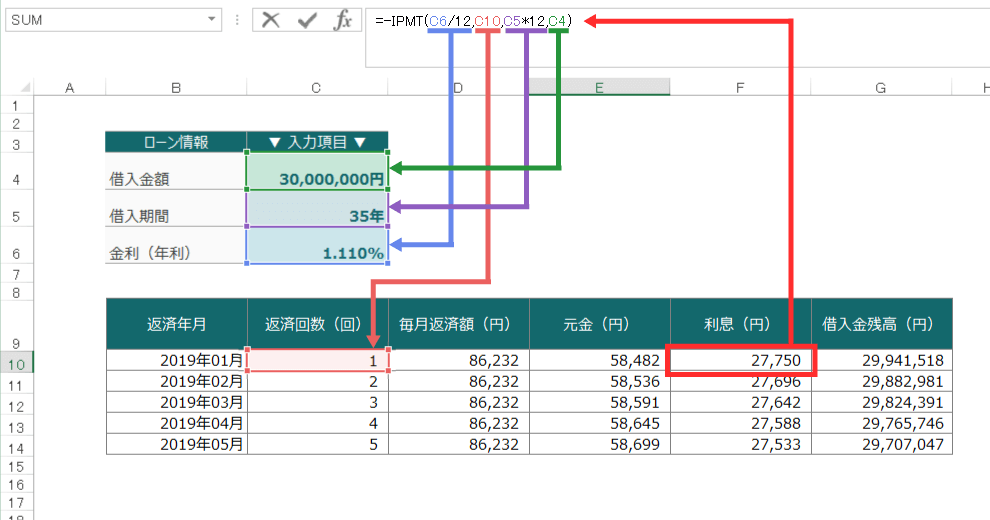
エクセルでは、このように該当するセルを参照させます。
例えば、1回目の利息分を計算する場合は、
で、「27,750円」が求められます。
30回目の利息分を計算する場合は、
と、回数を変えていけば、知りたい回数の利息分を計算できます。
計算式の注意点
IPMT関数もPMT関数と同じで、結果が「-(マイナス)」になります。
計算式に入力する際は、「-」をつけましょう。
PMT・PPMT・IPMT関数のうち使うのは2つだけ!
エクセル関数を使って、元利均等返済の「返済額」「元金」「利息」の計算方法を説明しましたが、エクセルで住宅ローンの返済予定表を作る場合は、PMT・PPMT・IPMT関数のうち2つだけを使ってください。
なぜかというと、それぞれ計算した場合に端数処理で誤差が生じます。
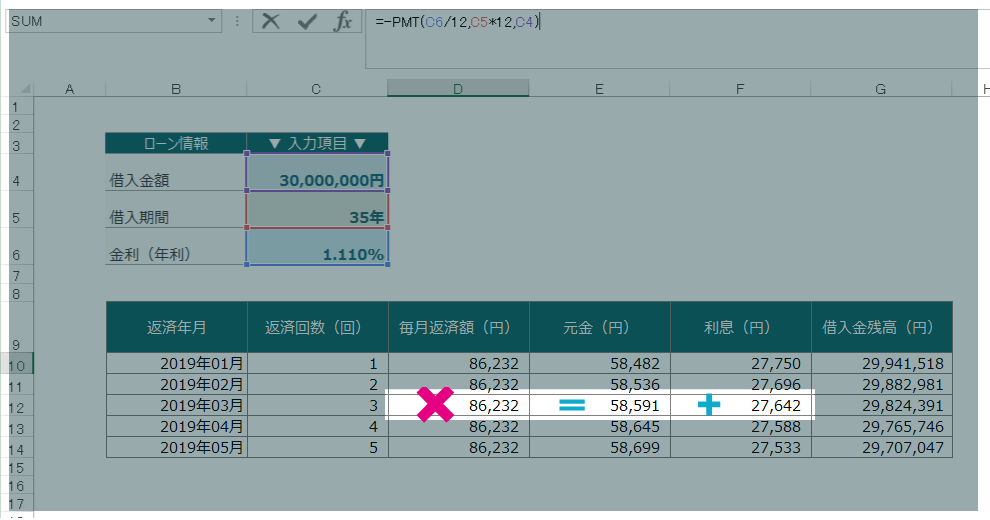
住宅ローンの返済額は、「元金+利息」で求められますが、例えば、3回目の元金と利息を合わせると、
と、PMT関数で計算した「86,232」よりも1円多く、計算が合いません。
セル上では、小数点以下を表示させていませんが、PMT・PPMT・IPMT関数の計算結果は、小数第10位まで値があります。
そのため、金額を合わせるには、ROUND・ROUNDDOWN・ROUNDUP関数のいずれかで「四捨五入・切捨て・切り上げ」をしてから整数にしましょう。
切り捨てには、ROUNDDOWN関数のほかにINT関数がありますが、INT関数はマイナス値で切り上げになる場合がありますので、利用しないほうがよいです。
更に、「返済額」「元金」「利息」のいずれかを、足し算あるいは引き算で求めると誤差が生じません。
元金均等返済のエクセル関数
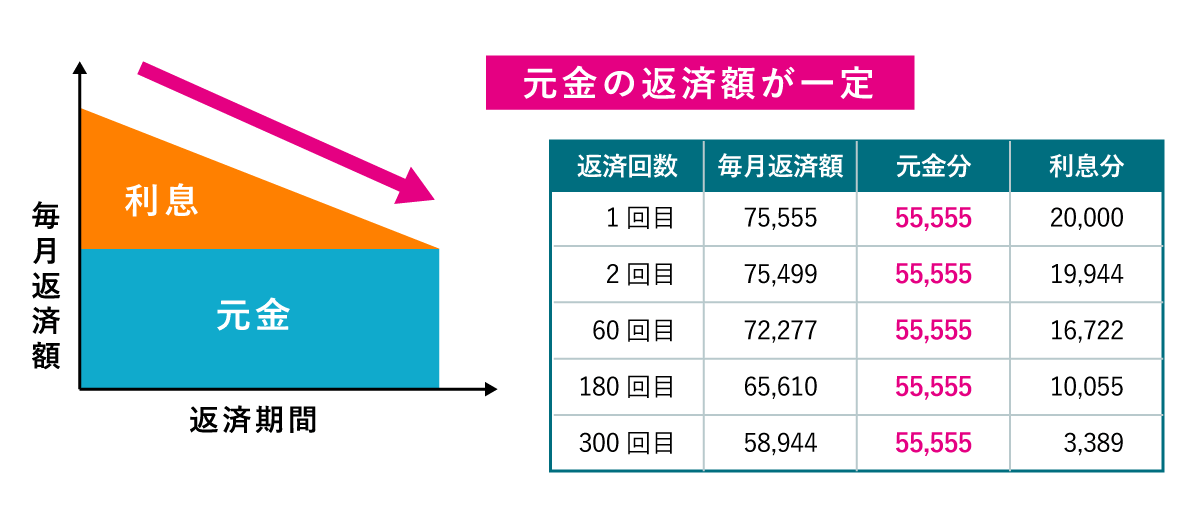
元金均等返済とは 『元金分を毎月均等に返済し、利息を含めて返済する方法』のことです。
毎月の返済額は、返済当初が最も高く、返済が進むと返済額が少なくなるのが特徴です。
元金均等返済で使うエクセル関数
元金均等返済で使うエクセル関数は、以下の1つです。
- ISPMT関数・・・n回目の利息分を計算
毎月の返済額と元金分は、四則計算で求められます。
毎月の元金分を求める「÷」
元利均等返済の元金分を求める際に「PPMT関数」を利用しましたが、元金均等返済は、元金が一定のため以下の計算式で簡単に求められます。
エクセルの計算式
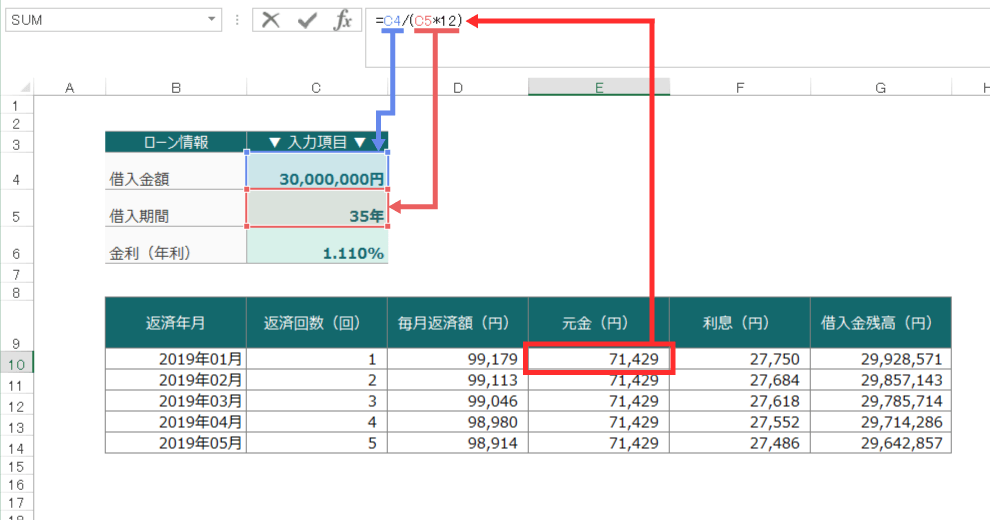
エクセルでは、このように該当するセルを参照させます。
こちらの例では、「借入金額3,000万円」「借入期間35年」の場合、
が、毎月の元金分となります。
毎月の利息分を求めるISPMT関数
ISPMT関数とは 『元金均等返済の1回あたりの利息分を求める関数』 のことです。
元金均等返済の利息分を求める場合は、ISPMT関数を利用します。
ISPMT関数の計算式は、以下の通りです。
利率・期間・現在価値
利率・期間・現在価値は、すべてPMT関数と内容は同じです。
期
期には、住宅ローン返済期間のうち何回目かを入力する点は、これまでと同じですが、回数の数え方に注意が必要です。
PPMT関数とIPMT関数では、返済回数が5回目なら「5」と入力しましたが、ISPMT関数では、1回目が「0」から始まります。
つまり、5回目の利息分を計算する場合は「4」を、25回目の利息分を計算する場合は「24」を入力します。
エクセルの計算
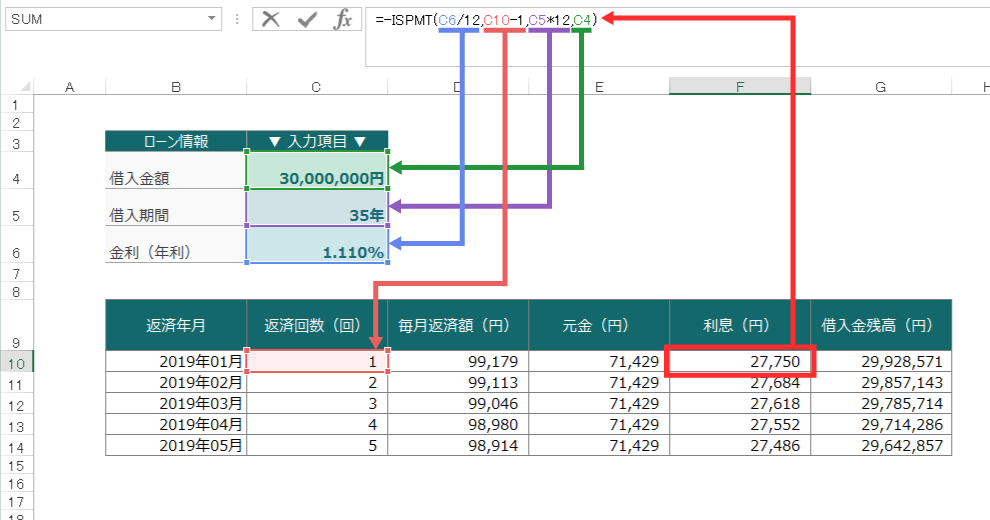
エクセルでは、このように該当するセルを参照させます。
例えば、1回目の利息分を計算する場合は、
で、「27,750円」が求められます。
15回目の利息分を計算する場合は、
と、回数を変えていけば、知りたい期の利息分を計算できます。
計算式の注意点
ISPMT関数もPMT・IPMT関数と同じで、結果が「-(マイナス)」になります。
計算式に入力する際は、「-」をつけましょう。
毎月の返済額を求める「+」
元金均等返済返済の毎月返済額は、元金と利息が計算できていますので、以下の計算式で簡単に求められます。
エクセルの計算式
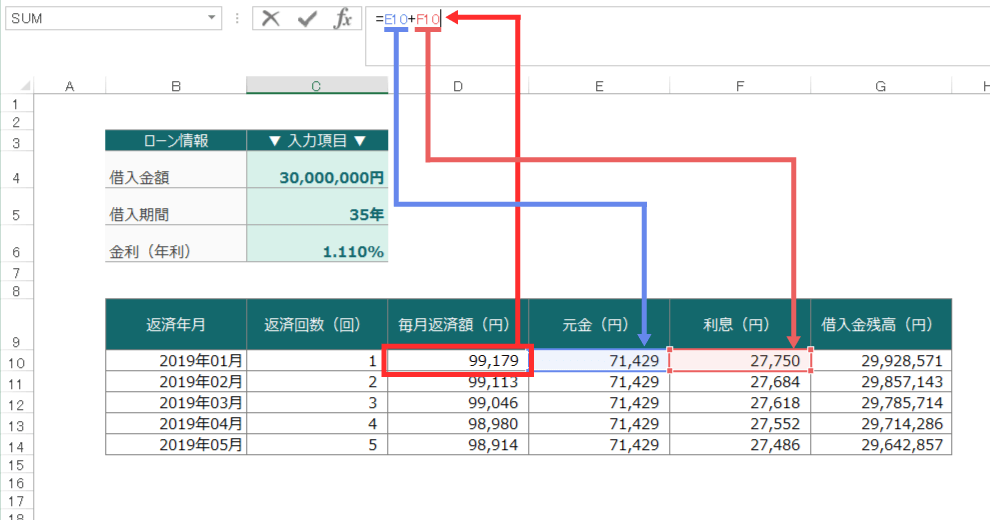
エクセルでは、このように該当するセルを参照させます。
例えば、1回目の「元金分71,429円」「利息分27,750円」から、1回目の返済額を計算すると、
となります。
元金均等返済でも「元金」「利息」が少数を含むと金額が生じますので、ROUND・ROUNDDOWN・ROUNDUP関数のいずれかで「四捨五入・切捨て・切り上げ」をしてから整数にしましょう。
エクセルの住宅ローン返済予定表テンプレート
エクセルの住宅ローン返済予定表テンプレートを無料で提供しています。
ここまで説明した関数を利用していますので、どのように返済予定表を作成すればよいか参考にしてください。
住宅ローン返済予定表テンプレートの詳しい使い方については【 元利均等返済と元金均等返済に対応したエクセルテンプレートの使い方 】でまとめています。

【エクセルファイルの特徴】
- 元利均等返済/元金均等返済対応のシミュレーター
- 指定した固定金利で自動計算(変動金利には対応していません)
- ボーナス払い対応(1回・2回選択可)
- 毎月返済分(A)・ボーナス払い分(B)・(A)+(B)別の年間返済額を確認できる
- 指定回数の「年数」「返済年月」「返済回数」「返済額」「元金」「利息」「借入金残高」を確認できる(ボーナス返済も同様)
- 最新金利情報ボタン
- 正確な端数処理で「返済額」「元金」「利息」の誤差0
- シートコピーでいくつもシミュレーション可能
まとめ
ここまで、こちらでは、エクセルを使って元利均等返済と元金均等返済の「返済額」「元金」「利息」の計算方法について、
解説しました。
住宅ローンの返済額を求める方法は、電卓以外にも色々あります。
- シミュレーションサイト
- エクセルの関数
- 返済額早見表(借入金額100万円当たりの毎月返済額)
- 電卓
- アプリ
じっくり比較検討したい方には、エクセルを使ったシュミレーションがお勧めです。
全体的にざっくり知りたい方は、シミュレーションサイトや電卓、アプリ、返済額早見表を使って求めたほうが早いです。
どれを利用しても結果はほぼ同じですので、現在ご自身が求めている情報を得られるものを利用しましょう。
その他の住宅ローン返済額を求める方法

【無料】元利均等返済と元金均等返済に対応したエクセルテンプレート
- テンプレートのダウンロード
- テンプレートの使い方
- シミュレーション結果の比較と計算根拠
- その他のシミュレーション方法

電卓を使った住宅ローンの計算方法!元利均等返済と元金均等返済に対応!
- 元利均等返済と元金均等返済の違い
- 住宅ローン返済額の計算式
- 電卓を使った簡単な計算方法
- 【おまけ】電卓が無くてもGoogle電卓で簡単に計算する方法
住宅ローン返済額早見表!100万円当たりの返済額の倍数で簡単計算!
- 元利均等返済と元金均等返済の違い
- 返済額早見表の計算式と注意点
- 元利均等返済の返済額早見表(毎月返済額)
- 元金均等返済の返済額早見表(1回目返済額)

すべて無料!住宅ローン計算アプリ厳選3選!
- 簡単操作でサクっと返済額を求めたい人向けアプリ
- 大まかな返済額と比較ができればいい人向けアプリ
- 繰り上げ返済をパターン別に比較した人向けアプリ
住宅ローンの基本の「き」

元利均等返済と元金均等返済の違いは?住宅ローン返済はどっちがお得?
- 元利均等返済と元金均等返済の違い
- 2つの返済方法のメリット・デメリット
- 元金均等返済に向いている人は、こんな方
- 元利均等返済に向いている人は、こんな方

